Radiation-II

THE VIEW FACTOR/SHAPE FACTOR

It is a purely geometric quantity and is independent of the surface properties and temperature. It is also known as configuration factor and angle factor.

The view factor from a surface i to a surface j is denoted by Fi → j or just $F_{ij}$, and is defined as

$F_{ij}$ = the fraction of the radiation leaving surface i that strikes surface j directly

$$F_{ij} = \frac{Q_{ij}}{Q_i}$$

Here,            $Q_{ij}$ =  fraction of rate of energy leaving surface i reaching surface j

                    Qi = Rate of total energy radiated by surface i

• In general, 0 ≤ $F_{ij}$ ≤ 1.

• The view factor from a surface to itself is zero for plane or convex surfaces and nonzero for concave surfaces.

Reciprocity Relation

$$\boxed{A_1F_{12} = A_2F_{21}}$$

Summation Rule

The sum of the view factors from surface i of an enclosure to all surfaces of the enclosure, including to itself, must equal unity.

$$\boxed{\sum^N_{j =1} F_{ij}  =1}$$

$F_{11} = 0$

$F{11} + F_{12} = 1$   (Summation Rule)

hence $F_{12} = 1$

$A_1F{12} = A_2F_{21}$   (Reciprocity Rule)

$F_{21} = \frac{A_1}{A_2}$

$F_{21} + F_{22} = 1$   (Summation Rule)  

$F_{22} = 1 - F_{21} = 1 - \frac{A_1}{A_2}$

Superposition Rule

The view factor from a surface i to a surface j is equal to the sum of the view factors from surface i to the parts of surface j. 

Note : The reverse of this is not true.

  $$F_{1(23)} = F_{12} + F_{13}$$

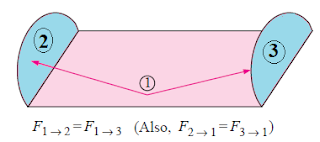Symmetry Rule

This Rule can be expressed as two (or more) surfaces that possess symmetry about a third surface will have identical view factors from that surface.

The Crossed-Strings Method

View Factors between Infinitely Long Surfaces is given by

$$F_{12} = \frac{(L_5 +L_6) -(L_3 + L_4)}{2*L_1}$$

$$F_{ij} = \frac{\sum (Crossed \quad Strings) - \sum (Uncrossed \quad Strings)}{2*(String \quad on \quad surface 'i')}$$

Net Radiation Heat Transfer to or from a Surface

Net Energy Leaving a Surface

The net energy leaving from the surface will be equal to the difference between the energy leaving a surface and the energy received by a surface 

$$Q_i = A_i(J_i -G_i)$$

$$J = ε E_b + ρG$$

If Surface is opaque, ρ = 1 – α 

J = ε Eb + (1 – α) G

we get,   $Q_i = \frac{E_b - J_i}{R_i}$ and $R_i = \frac{1-ε_i}{A_iε_i}$ is the surface resistance to the radiation.

Net Exchange Between Surfaces

The net rate of radiation heat transfer from surface i to surface j can be expressed as

$$Q_{ij} = A_iJ_iF_{ij} - A_jJ_jF_{ji}$$

$$Q_{ij} = \frac{J_i - J_j}{R_{ij}}$$

where $R_{ij}= \frac{1}{A_iF_{ij}}$ is the space resistance to the radiation.

Electrical circuit representation of two surfaces which can see each other nothing else

Total resistance      $R_t = \frac{1-ε_1}{ε_1A_1} + \frac{1}{A_1F_{12}} + \frac{1-ε_2}{ε_2A_2}$
$$Q_{12} = \frac{E_{b1} - E_{b2}}{R_t}$$

Radiation Shields

Assume two flat infinite long flate surfaces 1 and 2 have N shields in between.

Net Heat Transfer without any shield:

$$Q = \frac{A \sigma (T_1^4 - T_2^4)}{\frac{1}{ε_1} + \frac{1}{ε_2} -1}$$

Net Heat transfer with N shields

$$Q = \frac{A \sigma (T_1^4 - T_2^4)}{(\frac{1}{ε_1} + \frac{1}{ε_2} -1) + \sum^N_{j=1}(\frac{1}{ε_{j,1}} + \frac{1}{ε_{j,2}} -1) }$$

***

If you have any query, ask in comments.